| |
|
Basic Concepts
Review of the common concepts will lay the foundation for discussion of the conservation and accounting framework. Although these terms are familiar, it is instructive to explicitly state our definitions to avoid confusion in the following discussion.
System A system is any region in space or quantity of matter set aside for analysis. Everything not inside the system is in the surroundings. The system boundary is an infinitesimally thin surface, real or imagined, that separates the system from its surroundings. It has no mass and merely serves as a delineator of the extent of the system. Any system can be further subdivided into subsystems.
For modeling purposes, it is useful to classify systems according to the behavior of their boundaries. Using this approach we define three types of systems: closed, open, and isolated systems. The first two classifications specify whether a system can exchange mass with the surroundings. A closed system is a system whose boundary prevents mass transfer; thus a closed system has a fixed and unchanging mass. An open system is a system whose boundary allows mass transfer with the surroundings. (Traditionally, the closed system has been referred to as a control mass or sometimes just a system, and the open system has been referred to as a control volume.) The third classification applies to all interactions between a system and its surroundings. An isolated system is a system whose boundaries prevent any and all interactions with the surroundings. Thus, an isolated system exchanges nothing with its surroundings.
Property A propertyis any characteristic of a system that can be given a numerical value without regard to the history of the system. Properties are classified as either intensive or extensive. An intensive property has a value at a point and its value is independent of the extent or size of the system. (To talk about a value at a point, we assume that we are dealing with a continuum where a point is physically small enough to have a single value and large enough to contain sufficient particles that the value has statistical significance. This concept is described in most fluid mechanics' textbooks.) The value of an intensive property is typically a function of both its position within the system and time. An extensive property does not have a value at a point and its value depends on the extent or size of the system. The amount of an extensive property for a system can be determined by summing the amount of extensive property for each subsystem that comprises the system. The value of an extensive property for a system only depends upon time. Table 1 illustrates typical extensive properties and the related intensive property.
TABLE 1 Examples of Extensive and Intensive Properties
|
Extensive Property
|
Intensive Property
|
|
Symbol
|
Name
|
Units
|
Symbol
|
Name
|
Units
|
|
m
|
Mass
|
kg
|
|
|
|
|
q
|
Charge
|
C
|
|
|
|
|
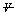
|
Volume
|
m3
|
u
|
Specific Volume
|
m3/kg
|
|
E
|
Energy
|
kJ
|
e
|
Specific Energy
|
kJ/kg
|
|
Ek
|
Kinetic Energy
|
kJ
|
ek = V 2/2
|
Specific Kinetic Energy
|
kJ/kg
|
|
P
|
Linear Momentum
|
kg×m/s
|
p = V
|
Velocity (Specific Linear Momentum)
|
m/s
|
|
S
|
Entropy
|
kJ/K
|
s
|
Specific Entropy
|
kJ/(K×kg)
|
| |
|
|
P
|
Pressure*
|
kPa
|
| |
|
|
T
|
Temperature*
|
K
|
|
*Specific intensive properties
|
An intensive property that has an extensive counterpart is called a specific intensive property, e.g. specific volume and volume. Temperature and pressure are two of the most familiar specific intensive properties.
Conserved Property Empirical evidence as codified by science has identified a class of extensive properties that can neither be created nor destroyed. An extensive property that satisfies this requirement is called a conserved property. The following five statements are equivalent and all characterize a conserved property.
· The amount of the extensive property in the universe is constant.
· The extensive property can be neither generated nor consumed within any system.
· The extensive property can be neither created nor destroyed.
· The amount of the extensive property in an isolated system is constant.
· The amount of the extensive property in a system plus the amount of the extensive property in the surroundings is constant.
Based on results of numerous experiments there are three conserved quantities: charge, linear momentum, and angular momentum. Conditions under which two other extensive properties: mass and energy, are more restricted, but widely applicable. In the absence of nuclear reactions, at speeds significantly less than the speed of light, and over time intervals that are long compared with intervals common in quantum mechanics, mass and energy are conserved as separate extensive properties. However, under more unusual conditions mass and/or energy are no longer conserved. First, if nuclear reactions are allowed, then a single extensive property that could be referred to as mass/energy is conserved. For nuclear reactions, Einstein showed that mass could be transformed to energy or vice versa via the E = mc2 relationship. Second, in the regime of quantum mechanics, Heisenberg's uncertainty principle, 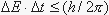 , asserts that the uncertainty in energy times the uncertainty in time must be less than Planck's constant divided by 2p. If the uncertainty in time is very small, the uncertainty in energy could be very large. Thus, conservation of energy could be violated for very small time intervals. Third, at speeds near the velocity of light, mass/energy must be redefined in order to be conserved. Despite the restrictions, five quantities: charge, linear momentum, angular momentum, mass and energy are conserved in a large number of situations. Conservation of these five quantities can be very useful in developing mathematical models for analysis of engineering artifacts. , asserts that the uncertainty in energy times the uncertainty in time must be less than Planck's constant divided by 2p. If the uncertainty in time is very small, the uncertainty in energy could be very large. Thus, conservation of energy could be violated for very small time intervals. Third, at speeds near the velocity of light, mass/energy must be redefined in order to be conserved. Despite the restrictions, five quantities: charge, linear momentum, angular momentum, mass and energy are conserved in a large number of situations. Conservation of these five quantities can be very useful in developing mathematical models for analysis of engineering artifacts.
It should be noted that the use of the concept of conservation in the conservation and accounting framework is slightly different that the use of conservation in physics. Traditionally in physics, the idea of conservation has been used as a modeling assumption for a specific problem. As used here, a conserved property is a statement about the way the world behaves in general. Conservation is never used as a modeling assumption. A property is either conserved or not.
In addition to conserved properties, there are other extensive properties for which we know limits on the generation/consumption terms. The classic example of this is the Second Law of Thermodynamics and its associated property entropy. Written as an accounting equation, we know that entropy can only be produced within a system. Furthermore in the limit of an internally reversible process, the entropy production rate reduces to zero.
State The state of a system is a complete description of a system in terms of its properties. Strictly speaking this requires knowledge of all the properties of a system at an instant in time; however, it turns out that we will often only need to know information about a few of the properties of a system to describe the behavior of a system. For some properties, we will discover that only a few need to be specified to uniquely determine the rest, e.g. the state postulate and the thermodynamic properties of a system. In other cases, we will discover that the problem at hand only requires knowledge of a limited number of properties, e.g., velocity of a falling object in a gravitational field with negligible air resistance.
Process When a system undergoes a change in state, we say that the system has undergone a process. It is frequently the goal of engineering analysis to predict the behavior of a system, i.e., the path of states that result, when it undergoes a specified process. Processes can be classified in three ways based on the time interval involved: finite-time, transient, and steady-state processes. A finite-time process involves a change in state over an explicitly or implicitly defined time interval of finite duration. Problems that talk of initial and final states typically fall in this category. Mathematically, the analysis of a finite-time process often involves solving a definite integral to determine the change in a property of the system. A transient process involves a finite, yet changing time interval. Problems that consider how the state of a system evolves or changes with time fall in this category. Mathematically, the analysis of a transient process often involves the solution of an ordinary differential equation to determine the variation of a system property with time. A steady-state process is a special type of transient process in which the intensive properties of the system are independent of time; thus, time is no longer a variable in the analysis. Typically, the analysis of a system undergoing a steady-state process involves the solution of a set of algebraic equations. If the properties of a system undergo steady-periodic variations, it is frequently assumed that the system undergoes a steady-state process on a time-averaged basis.
Accounting Principle Now that we have defined the basic concepts, we can discuss the accounting principle. Experience has taught us that the extensive properties of a system, i.e. the amount of an extensive property within a system, may change with time. Based on our observations, we postulate that this change can only occur by two mechanisms: (1) transport of the extensive property across the system boundary and (2) generation (production) or consumption (destruction) of the extensive property inside the system. Thus, we can relate the change of an extensive property within a system to the amount of the extensive property transported across the boundary and the amount of the extensive property generated (or consumed) within the system. This simple balance is referred to as the accounting principle for an extensive property. Although this principle can be applied to a system for any extensive property, it will be especially useful for those properties that are conserved.
Two forms of the accounting statement
There are two forms of the conservation/accounting statements: the accumulation form and the rate form.
In the accumulation form, the time period used in the analysis is finite. When accounting for the input and output, you compute the total amount that enters in the time period and subtract the total amount that exits in the same time. The accounting statement is total amount that came in - total amount that went out + total amount generated - total amount consumed = amount inside at the final time - amount inside at the beginning.
The advantages of using an accumulation form of the conservation or accounting laws is that you will end up with either algebra or integral equations. The disadvantages of the accumulation form of the law is that it is not always possible to determine the amount of stuff entering or exiting from the system.
In the rate form you add the rate that stuff enters subtract the rate that stuff leaves add the rate that it is generated subtract the rate that it is consumed and set this equal to the rate that it changes inside the boundary. The advantage of the rate form of the law is that the laws of physics generally make it easy to find the rates that things are happening. The disadvantage of the rate form is that it generates differential equations. To apply the rate form of the law, you should choose an infinitesimally small time period.
When applied to a system over a finite-time interval, the finite-time (or accumulation) form of the accounting principle says that for any extensive property the

or the
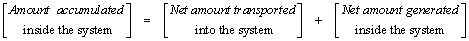
For a generic extensive property B, Eq. can be written symbolically as

where Bsys is the amount of property B inside the system, Btransport is the amount of property B that crosses the system boundary, and Bgenerate/consume is the amount of property B generated/consumed.
When applied to a system for an infinitesimal time interval the accounting principle is written in terms of rates (rate-form of the accounting principle) and says that for any extensive property the

or the

For a generic extensive property B, Eq. can be written mathematically as

The mathematical relationship between the finite-time form and the rate form can easily be developed by dividing the finite-time form through by the time interval Dt and taking the limit as Dt ® 0.
Although the accounting principle can be applied for any extensive property, it is most useful when the transport and generation/consumption terms have physical significance. The most useful applications of this principle occur when something is known a priori about the generation/consumption term. For conserved extensive properties the equations that apply the accounting principle are significantly simpler. In the finite-time form the equations become

Equation can be expressed symbolically for a generic extensive property B as

Back
|
|
References
-
Grinter, L.E. (Chair), Report on Evaluation of Engineering Education, American Society for Engineering Education, Washington, DC, 1955.
-
Harris, Eugene M. DeLoatch, William R. Grogan, Irene C. Peden, and John R. Whinnery, "Journal of Engineering Education Round Table: Reflections on the Grinter Report," Journal of Engineering Education, Vol. 83, No. 1, pp. 69-94 (1994) (includes as an Appendix the Grinter Report, issued in September, 1955).
-
Glover, Charles, J., and Carl A. Erdman, "Overview of the Texas A&M/NSF Engineering Core Curriculum Development," Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 363-367
-
Glover, Charles J., K. M. Lunsford, and John A. Fleming, TAMU/NSF Engineering Core Curriculum Course 1: Conservation Principles in Engineering, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 603-608
-
Glover, Charles J., K. M. Lunsford, and John A. Fleming, Conservation Principles and the Structure of Engineering, 3rd edition, New York: McGraw-Hill College Custom Series, 1992
-
Pollock, Thomas C., TAMU/NSF Engineering Core Curriculum Course 2: Properties of Matter, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 609-613
-
Pollock, Thomas C., Properties of Matter, 3rd edition, New York: McGraw-Hill College Custom Series, 1992
-
Everett, Louis J., TAMU/NSF Engineering Core Curriculum Course 3: Understanding Engineering via Conservation, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 614-619
-
Everett, Louis J., Understanding Engineering Systems via Conservation, 2nd edition, New York: McGraw-Hill College Custom Series, 1992
-
Glover, Charles J. and H. L. Jones, TAMU/NSF Engineering Core Curriculum Course 4: Conservation Principles for Continuous Media, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992 Conference, pp. 620-624
-
Glover, C. J. and H. L. Jones, Conservation Principles for Continuous Media, 2nd edition, New York: McGraw-Hill College Custom Series, 1992
-
Erdman, Carl A., Charles J. Glover, and V. L. Willson, Curriculum Change: Acceptance and Dissemination, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 368-372
-
B. A. Black, From Conservation to Kirchoff: Getting Started in Circuits with Conservation and Accounting, Proceedings of the 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Griffin, Richard B., Louis J. Everett, P. Keating, Dimitris C. Lagoudas, E. Tebeaux, D. Parker, William Bassichis, and David Barrow, "Planning the Texas A&M University College of Engineering Sophomore Year Integrated Curriculum," Fourth World Conference on Engineering Education, St. Paul, Minnesota, October 1995, vol. 1, pp. 228-232.
-
Everett, Louis J., "Experiences in the Integrated Sophomore Year of the Foundation Coalition at Texas A&M," Proceedings, 1996 ASEE National Conference, Washington, DC, June 1996
-
Richards, Donald E., Gloria J. Rogers, "A New Sophomore Engineering Curriculum -- The First Year Experience," Proceedings, 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Heenan, William and Robert McLaughlan, "Development of an Integrated Sophomore Year Curriculum, Proceedings of the 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Mashburn, Brent, Barry Monk, Robert Smith, Tan-Yu Lee, and Jon Bredeson, "Experiences with a New Engineering Sophomore Year, Proceedings of the 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Everett, Louis J., "Dynamics as a Process, Helping Undergraduates Understand Design and Analysis of Dynamics Systems," Proceedings, 1997 ASEE National Conference,
-
Doering, E., Electronics Lab Bench in a Laptop: Using Electronics Workbench to Enhance Learning in an Introductory Circuits Course, Proceedings of the 1997 Frontiers in Education Conference, November 1997
-
Cornwell, P., and J. Fine, Mechanics in the Rose-Hulman Foundation Coalition Sophomore Curriculum, Proceedings of the Workshop on Reform of Undergraduate Mechanics Education, Penn State, 16-18 August 1998
-
Cornwell, P., and J. Fine, Mechanics in the Rose-Hulman Foundation Coalition Sophomore Curriculum, to appear in the International Journal of Engineering Education
-
Cornwell, P. and J. Fine, Integrating Dynamics throughout the Sophomore Year, Proceeedings, 1999 ASEE Annual Conference, Charlotte, North Carolina, 20-23 June 1999
-
Burkhardt, H. "System physics: A uniform approach to the branches of classical physics." Am. J. Phys. 55 (4), April 1987, pp. 344350.
-
Fuchs, Hans U. Dynamics of Heat. Springer-Verlag, New York, 1996.
Back
|
 |
 |
© 2001 Foundation Coalition. All rights reserved. Last modified
|
 |
| |
|