| |
|
Formulating the Physical Laws in the Conservation and Accounting Framework
To help students begin to see the common features of the basic laws of physics and to provide a framework for problem solving it is useful to restate all of the basic laws in terms of the CAF. Answering four questions for each extensive property of interest provides the form of the physical law in the CAF:
(1) What is it?
(2) How can it be stored inside the system?
(3) How can it be transported across the system boundary? Students need to understand and apply the mechanisms through which an extensive property can cross the boundary. For example if you are counting something like energy, you will need to know all of the ways that energy can cross a boundary and determine which, if any, are applicable to the situation at hand.
(4) How can it be generated or consumed inside the system? In addition to transport mechanisms, students need to understand and apply knowledge about when and how an extensive property can be created or consumed. For example if you are counting positive charge, then you need to know that positive charge can be created by ionization processes or consumed by recombination processes. When a quantity can neither be created nor consumed we say that quantity is conserved. Again, this definition is different from the definition used in many textbooks on physics and engineering science.
Once students have answered these four questions, then they can adapt the accounting principle for each extensive property and demonstrate the underlying similarities between the fundamental principles of physics. Consider the extensive properties mass and linear momentum. Table 2 provides answers to each of these questions for mass, and Table 3 provides answers for linear momentum.
Table 2: Accounting Principle for Mass
|
Question
|
Answer
|
|
What is it?
|
The mass of an object is a measure of the amount of matter in the object.
|
|
How can it be stored inside the system?
|
If there is any matter inside the system, then the system has mass. Given a system of volume  and information about the density r of the matter in the system, then the system mass msys can be calculated from the integral over the system volume and information about the density r of the matter in the system, then the system mass msys can be calculated from the integral over the system volume
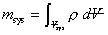
where r is the mass density of the substance.
|
|
How can it be transported across the system boundary?
|
Mass can only be transported across a system boundary when atoms or molecules physically move across the system boundary between the system and the surroundings. In general, this transport occurs due to either gross fluid motion or through molecular diffusion.
In either case, we can define the mass flow rate to be the rate at which mass crosses a boundary per unit time. The symbol adopted for the mass flow rate will be a dotted lower-case m,  . .
|
|
How can mass be generated or consumed within the system?
|
Empirical evidence has repeated demonstrated that for the conditions of most engineering applications, mass cannot be created or destroyed within the boundaries of a system. Thus mass is conserved!
|
|
Accounting Equation for Mass (Conservation Equation)
|
|
Rate form of
Conservation of Mass
|

where  is the mass flow rate and the summations are over all the inlets and outlets. is the mass flow rate and the summations are over all the inlets and outlets.
|
|
Finite-time form of
Conservation of Mass
|

where  , the amount of mass that flows across the boundary in the time interval. , the amount of mass that flows across the boundary in the time interval.
|
|
|
|
Table 4 summarizes the rate-form of the accounting principle for six extensive properties that are commonly used in engineering analysis. As students attempt to solve engineering problems, they are often confronted with relating changes within a system to things that happen to the system. The accounting equation provides an explicit way to relate these things. It in fact is the only mechanism for relating system interactions that are spatially separated on the boundary of a system. For example, if I consider a compressed spring, how are the forces acting on the ends of the spring related? If we take the stationary spring as the system and apply conservation of linear momentum, we see that the linear momentum of the system is constant (in fact it is zero) and the forces acting on the system boundary must be equal in magnitude and opposite in direction.
This authors prejudice is to focus on the rate-form of the equations because it is an easy matter to go from the rate-form to the finite-time form by integrating both sides with respect to time.
Table 3: Accounting Principle for Linear Momentum
|
Question
|
Answer
|
|
What is linear momentum?
|
Linear momentum of a particle is the product of mass and velocity: P = mV
|
|
How can linear momentum be stored inside the system?
|
If there is any matter inside the system and that mass has velocity, then the system has linear momentum.
For a system of n discrete particles, then the linear momentum of the system of particles is

For a continuous system of volume  with density r and velocity V, both functions of position and time, the system linear momentum can be calculated from the integral over the system volume with density r and velocity V, both functions of position and time, the system linear momentum can be calculated from the integral over the system volume

|
|
How can linear momentum be transported across the system boundary?
|
Linear momentum can be transported by two mechanisms: forces and mass-transport of linear momentum.
For a system, the transport rate of linear momentum by an external force is Fexternal. External forces can be classified as either body forces, like weight, or surface (or contact) forces.
For an open system, every mass that crosses the system boundary carries with it linear momentum due to its velocity. The mass transport rate of linear momentum is the product of the mass flow rate and the velocity,  . .
|
|
How can linear momentum be generated or consumed within the system?
|
Empirical evidence has repeatedly demonstrated that linear momentum cannot be created or destroyed within the boundaries of a system. Thus linear momentum is conserved!
|
|
Accounting Equation for Linear Momentum (Conservation Equation)
|
|
Rate form
of
Conservation of Linear Momentum
|

where 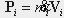 and and 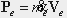 are the mass-transport rates of linear momentum at the boundary and the summations are over all the inlets and outlets. are the mass-transport rates of linear momentum at the boundary and the summations are over all the inlets and outlets.
|
|
Finite-time form
of
Conservation of Linear Momentum
|
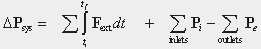
where 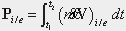 , the amount of mass that flows across the boundary in the time interval. , the amount of mass that flows across the boundary in the time interval.
|
|
|
|
Table 4 summarizes the rate-form of the accounting principle for six extensive properties that are commonly used in engineering analysis. As students attempt to solve engineering problems, they are often confronted with relating changes within a system to things that happen to the system. The accounting equation provides an explicit way to relate these things. It in fact is the only mechanism for relating system interactions that are spatially separated on the boundary of a system. For example, if I consider a compressed spring, how are the forces acting on the ends of the spring related? If we take the stationary spring as the system and apply conservation of linear momentum, we see that the linear momentum of the system is constant (in fact it is zero) and the forces acting on the system boundary must be equal in magnitude and opposite in direction.
Table 4 - Rate-form of the Basic Laws
|
Mass
(Conserved)
|
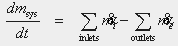
|
|
The rate at which mass is accumulated within the system is equal to the difference between the rate at which mass enters the system and the rate at which mass leaves the system. The symbol 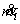 is a conventional symbol for mass rate into a system. The symbol is a conventional symbol for mass rate into a system. The symbol 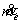 is a conventional symbol for mass rate exiting a system. is a conventional symbol for mass rate exiting a system.
|
|
Charge
(Conserved)
|
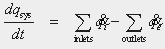
|
|
The rate at which charge is accumulated within the system is equal to the difference between the rate at which change enters the system and the rate at which charge leaves the system.
|
|
Linear
Momentum
(Conserved)
|
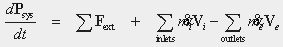
|
|
The rate at which linear momentum is accumulated within the system is equal to the sum of the external forces acting upon the system plus the rate at which mass entering the system adds linear momentum minus the rate at which mass leaving the system subtracts linear momentum. For a closed system, i.e., a system that does not exchange mass with its surroundings, the rate law simplifies to a statement of Newtons second law.
|
|
Angular
Momentum
(Conserved)
|
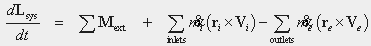
|
|
The rate at which angular momentum is accumulated within the system is equal to the sum of the external moments (or torques) acting upon the system plus the rate at which mass entering the system adds angular momentum minus the rate at which mass leaving the system subtracts angular momentum. For a closed system, i.e., a system that does not exchange mass with its surroundings, the rate law simplifies to a statement that the rate at which angular moment accumulates within a system is equal to the sum of external moments (or torques) acting on the system.
|
|
Energy
(Conserved)
|
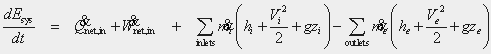
|
|
The rate at which energy is accumulated within the system is equal to the net rate of heat flow into the system plus the net work done on the system plus the rate at which mass entering the system adds energy (through either potential, kinetic or internal energy{?}) minus the rate at which mass leaving the system subtracts energy. {Do we need comments about sign conventions?}
|
|
Entropy
|

|
Another approach to understanding the CAF is to compare it to the discipline of system dynamics. In the later discipline, much emphasis is placed on energy storage and transfer by identifying "through" variables and "across" variables. How are the "through" and "across" variables related to the six intensive properties in Table 4? To facilitate the comparison, consider a simple, linear, ideal spring as a closed system. Application of the conservation of linear momentum and shows that the forces at the two ends of the spring

are opposite direction and differ in magnitude by the rate at which linear momentum is accumulated in the spring. If the spring is stationary or the spring mass is negligible, the forces (transport rates of momentum) are equal and opposite in direction. Application of the conservation of energy shows that the rate at which energy accumulates in the system is given by

If the force F2 is rewritten as the difference between the rate at which linear momentum is accumulating and the force F1, then the conservation of energy equation may be rewritten.

If the rate at which linear momentum accumulates is zero, e.g., if the spring is stationary or massless, then the rate at which energy accumulates is equal to the force applied to the spring dotted with the difference in the velocities between the two ends of the spring. In a systems dynamics framework, , the force is the "through" variable for energy transfer. The through variable exists if and only if the spring does not accumulate linear momentum. Also, in a systems dynamics framework, the velocity difference between the two ends of the spring is the "across" variable and is related to the rate at which energy accumulates in the spring. Typically, the "across" variable is really just the difference between the values of an intensive property measured at two points on the system boundary. So the "through" and "across" variables in a systems dynamics framework can be obtained from the accounting equations for the intensive properties in Table 4..
Back
|
|
References
-
Grinter, L.E. (Chair), Report on Evaluation of Engineering Education, American Society for Engineering Education, Washington, DC, 1955.
-
Harris, Eugene M. DeLoatch, William R. Grogan, Irene C. Peden, and John R. Whinnery, "Journal of Engineering Education Round Table: Reflections on the Grinter Report," Journal of Engineering Education, Vol. 83, No. 1, pp. 69-94 (1994) (includes as an Appendix the Grinter Report, issued in September, 1955).
-
Glover, Charles, J., and Carl A. Erdman, "Overview of the Texas A&M/NSF Engineering Core Curriculum Development," Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 363-367
-
Glover, Charles J., K. M. Lunsford, and John A. Fleming, TAMU/NSF Engineering Core Curriculum Course 1: Conservation Principles in Engineering, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 603-608
-
Glover, Charles J., K. M. Lunsford, and John A. Fleming, Conservation Principles and the Structure of Engineering, 3rd edition, New York: McGraw-Hill College Custom Series, 1992
-
Pollock, Thomas C., TAMU/NSF Engineering Core Curriculum Course 2: Properties of Matter, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 609-613
-
Pollock, Thomas C., Properties of Matter, 3rd edition, New York: McGraw-Hill College Custom Series, 1992
-
Everett, Louis J., TAMU/NSF Engineering Core Curriculum Course 3: Understanding Engineering via Conservation, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 614-619
-
Everett, Louis J., Understanding Engineering Systems via Conservation, 2nd edition, New York: McGraw-Hill College Custom Series, 1992
-
Glover, Charles J. and H. L. Jones, TAMU/NSF Engineering Core Curriculum Course 4: Conservation Principles for Continuous Media, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992 Conference, pp. 620-624
-
Glover, C. J. and H. L. Jones, Conservation Principles for Continuous Media, 2nd edition, New York: McGraw-Hill College Custom Series, 1992
-
Erdman, Carl A., Charles J. Glover, and V. L. Willson, Curriculum Change: Acceptance and Dissemination, Proceedings, 1992 Frontiers in Education Conference, Nashville, Tennessee, 11-14 November 1992, pp. 368-372
-
B. A. Black, From Conservation to Kirchoff: Getting Started in Circuits with Conservation and Accounting, Proceedings of the 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Griffin, Richard B., Louis J. Everett, P. Keating, Dimitris C. Lagoudas, E. Tebeaux, D. Parker, William Bassichis, and David Barrow, "Planning the Texas A&M University College of Engineering Sophomore Year Integrated Curriculum," Fourth World Conference on Engineering Education, St. Paul, Minnesota, October 1995, vol. 1, pp. 228-232.
-
Everett, Louis J., "Experiences in the Integrated Sophomore Year of the Foundation Coalition at Texas A&M," Proceedings, 1996 ASEE National Conference, Washington, DC, June 1996
-
Richards, Donald E., Gloria J. Rogers, "A New Sophomore Engineering Curriculum -- The First Year Experience," Proceedings, 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Heenan, William and Robert McLaughlan, "Development of an Integrated Sophomore Year Curriculum, Proceedings of the 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Mashburn, Brent, Barry Monk, Robert Smith, Tan-Yu Lee, and Jon Bredeson, "Experiences with a New Engineering Sophomore Year, Proceedings of the 1996 Frontiers in Education Conference, Salt Lake City, Utah, 6-9 November 1996
-
Everett, Louis J., "Dynamics as a Process, Helping Undergraduates Understand Design and Analysis of Dynamics Systems," Proceedings, 1997 ASEE National Conference,
-
Doering, E., Electronics Lab Bench in a Laptop: Using Electronics Workbench to Enhance Learning in an Introductory Circuits Course, Proceedings of the 1997 Frontiers in Education Conference, November 1997
-
Cornwell, P., and J. Fine, Mechanics in the Rose-Hulman Foundation Coalition Sophomore Curriculum, Proceedings of the Workshop on Reform of Undergraduate Mechanics Education, Penn State, 16-18 August 1998
-
Cornwell, P., and J. Fine, Mechanics in the Rose-Hulman Foundation Coalition Sophomore Curriculum, to appear in the International Journal of Engineering Education
-
Cornwell, P. and J. Fine, Integrating Dynamics throughout the Sophomore Year, Proceeedings, 1999 ASEE Annual Conference, Charlotte, North Carolina, 20-23 June 1999
-
Burkhardt, H. "System physics: A uniform approach to the branches of classical physics." Am. J. Phys. 55 (4), April 1987, pp. 344350.
-
Fuchs, Hans U. Dynamics of Heat. Springer-Verlag, New York, 1996.
Back
|
 |
 |
© 2001 Foundation Coalition. All rights reserved. Last modified
|
 |
| |
|